CAT Geometry : An alternate approach to find area 

A lot of questions in CAT and other management entrance exams are from Geometry and that too, from the topic called AREA.

Many questions are based on finding the area of triangle, circles and quadrilaterals etc. Most of these questions can be solved in various ways. There is always a traditional method to solve such problems but the problem which most of the aspirants encounter in geometry is that they are not able to apply the theory/theorems when it is required.

Here I am discussing an easy approach to solve a certain type of questions based on finding the area of the desired geometrical figure.

Let’s start with the question itself:

Example 1: In the triangle PQR (refer to the figure), S is the midpoint of PQ, ST $\bot $ PR, UR $\bot $ PR, and the area of ∆PQR is 36 sq. Units . Find the area of ∆PTU?

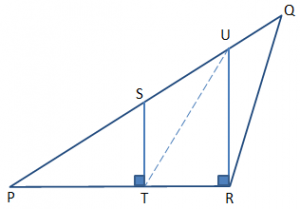
Won’t it be a good idea to try the above problem before going ahead?

---

Online CAT 2023 Course [VIDEO + LIVE session]

---

If you are done with your effort and got the answer congratulations to you J. In case you are finding it difficult to comprehend let me assure you that its not that difficult as it seems. By the end of the article you would be in a position to attempt such questions with ease J

Lets discuss some theorems which are handy for solving such problems.

We all know that

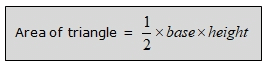
Theorem 1: Triangles with the same base and between same parallel lines have equal areas.

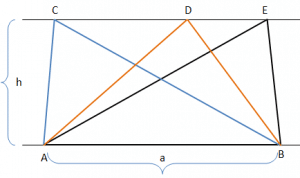
In the above figure for all three triangles ABC, ABD and ABE, the base i.e. AB and the height is same hence

[Area] ABC = [Area] ABD = [Area] ABE

 Theorem 2: If two triangles have the same base, the ratio of the areas is the ratio of the heights.

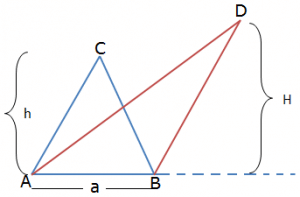
In the above figure AB is the common base, hence $\frac{Area\ of\ \Delta ABC}{Area\ of\ \Delta ABD}=\frac{h}{H}$

 Corollary:  If two triangles have the same height, the ratio of the areas is the ratio of the bases.

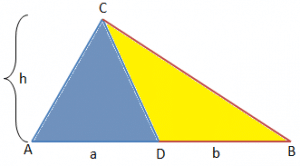
$\frac{Area\ of\ \Delta ACD}{Area\ of\ \Delta CDB}=\frac{a}{b}$

Theorem 3: In any Trapezium ABCD (refer figure), AB || CD, O is the intersection of diagonals AD and BC then,

Area of triangle AOC = Area of Triangle BOD

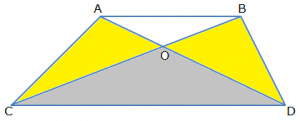
Proof:

Since AB||CD, from Theorem 1, we conclude that

Area of ∆ACD = Area of ∆BCD

Or Area of ∆AOC + Area of ∆COD = Area of ∆COD + Area of ∆BOD

Area of ∆ AOC = Area of ∆ BOD {since triangle COD is common}

Theorem 4:

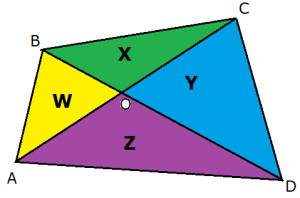
In any quadrilateral ABCD, with AC and BD as diagonals intersecting at O. Let

Area of ∆ AOB = W

Area of ∆ BOC = X

Area of ∆ COD = Y

Area of ∆ AOD = Z then,

W.Y =X.Z i.e.

Area of ∆ AOB x Area of ∆ COD = Area of ∆ BOC x Area of ∆ AOD

Note: The above relation can easily be proven with the help of theorem 2 as discussed above. I am leaving the proof for you all. Try it J

Now let’s visit the question which I asked in the beginning.

Question: In the triangle PQR (refer to the figure), S is the midpoint of PQ, ST $\bot $ PR, UR $\bot $ PR, and the area of ∆PQR is 36 sq. Units . Find the area of ∆PTU?

Solution:

Observe that ST||UR and STRU is a trapezium. Join SR, the figure looks like fig 1.1

Fig 1.1

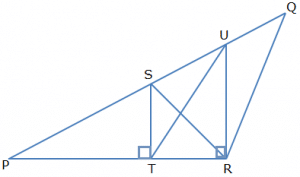
Fig 1.2

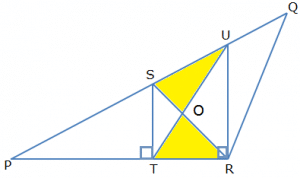
From Theorem 3, we find that area of ∆SOU = area of ∆TOR,

Also the area of ∆PTU = area of quad PTOS + area of ∆SOU

Or area of ∆PTU =  area of quad PTOS + area of ∆TOR

Or area of ∆PTU =  area of ∆PRS

Since S is the midpoint of triangle PQR, and RS is the median then,

Area of triangle PRS = $\frac{1}{2}\times Area\ of\ \Delta PQR$ = ½x36 = 18 sq. Units.

Example 2: In the adjacent figure ABCD is a square with side 15 cm. DEFG is another square with G lying on AD, find the area of the shaded region?

 

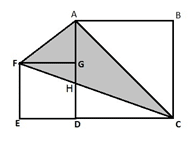
Solution:

Let FC intersect AD at H.

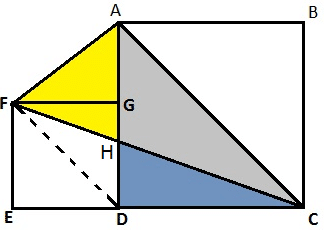
Join FD, we find FD||AC, also DFAC is a trapezium.

Applying theorem 3 we get Area of ∆FHA = Area of ∆CHD

Therefore, Area of ∆AFC = Area of ∆AHC + Area of ∆DHC = Area of ∆ADC = $\frac{1}{2}\times area\ of\ square\ ABCD$= $\frac{1}{2}\times {{15}^{2}}=112.5\ c{{m}^{2}}$

Example 3: In a triangle ABC with AB = 14 cm, D and E are points on BC and AC respectively such that BE and AD intersect at point F and the area of ∆ BFD = area of ∆ AFE. Also BD:DC = 2:5. Find the length of DE?

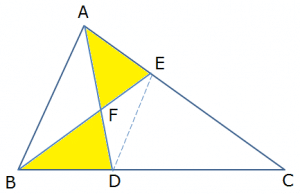
Solution:

Refer to the diagram,

Joining DE we observe that in a quadrilateral ABDE, since the area of ∆ BFD = area of ∆ AFE from Theorem 3, we conclude that DE is parallel to AB. Therefore by similar triangle concept,  ∆ CDE is similar to ∆ CBA with corresponding sides in the ratio:

BC: DC = (2+5): 5 = 7:5,

Therefore $\frac{DE}{AB}=\frac{5}{7}$

Hence the length of DE = $\frac{5}{7}\times 14=10\ cm$

Example 4: As shown in the figure, ABCD is a parallelogram AC and BE intersects at F. Area of ∆ CEF = 6 cm² and ∆ BCF = 9 cm². Find the area of quadrilateral ADEF?

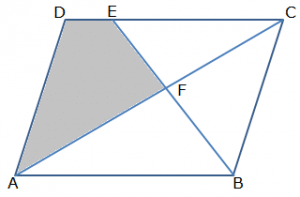
Solution:

Join AE. ABCE is a trapezium therefore from theorem 3, Area of∆ BCF = ∆ AFE = 9 cm²

Applying theorem 4 in ABCE we get,

Area of ∆ AFB x Area of ∆ EFC = Area of ∆ AFE x Area of ∆ BFC

Or  Area of ∆ AFB x 6 = 9 x 9

Or Area of ∆ AFB = 27/2 cm²

Area of ∆ ABC = Area of ∆ ADC = 9 + 27/2 = 22.5 cm²

Therefore Area of ADEF = Area of ∆ ADC – Area of ∆ EFC