The right approach to learn Geometry for CAT Exam (Part -1)

Geometry problems are an integral part of any aptitude based test like CAT. In recent CAT papers, around 7 questions have been consistently appearing in the quantitative aptitude section. I have been mentoring students for CAT exam over a decade. I have observed that each year, a good number of students face some peculiar problems in attempting geometry questions. They are:

1. In spite of knowing all the theorems, they are unable to identify the right concepts and the order in which those concepts should be applied to get to the solution.
2. Poor sense of symmetry / Visualization
3. Lack of construction concepts

In this article, I will discuss the first issue. The other two issues will be discussed in the subsequent articles.

We all are aware of the various theorems and concepts related to geometry. Once we start learning geometry, the first thing we do is to get hold of these theorems and concepts followed by some elementary problems which can be solved by using these concepts directly. In this way, we not only understand the concepts/theorems but also their applications.

This is how we generally learn the concepts of geometry. But, the problem occurs when you come across an independent geometry question. Often, you are clueless about the right concepts to be applied. This creates doubts in your mind about your ability to handle geometry problems, something that often results in demotivation and loss of interest in the subject. You wonder why is it that in spite of knowing all the concepts, you are not able to solve the questions.

One thing that needs to be understood is that the learning of geometry does not end with the understanding of the concepts and solving some easy problems based on those concepts. To handle geometry problems comprehensively, you must practice a variety of high difficulty problems that can be solved only by multiple concepts.

Each time you fail to solve a high difficulty question, you must refer to the solution and pay attention to the key concepts used and the structure/flow of the solution. Next time when you come across similar questions, you must recall the approach to solve such problems.  Use the process to group the types of questions based on the approach and key concepts.

This process of grouping questions based on similar key concepts are not restricted to geometry only. It can be extended to all other topics within the Quantitative Aptitude section. Therefore, I have deliberately structured my online CAT Quant Course on a similar line.

Let me take an example to make you understand what do I mean by learning the approach and grouping of similar questions.

Question 1: A circle with radius 2 is placed against the right angle. Another smaller circle is also placed as shown in the adjoining figure. What is the radius of the smaller circle? [CAT 2004]

Solution:

AB = AK = 2, therefore Quadrilateral ABCD is a square.

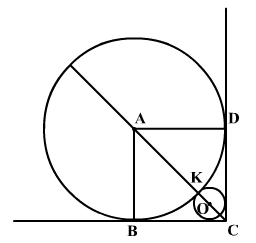
i.e., AC = 2$\surd 2$, implies KC = AC – AK = $2\sqrt{2}-2$

Let the centre of the smaller circle be O and let its radius be x.

i.e., OC = x$\surd 2$ and KC = KO+OC = x+x$\surd 2$

therefore, x + x$\surd 2$ = 2$\sqrt{2}-2$

i.e., x = $\frac{2\sqrt{2}-2}{1+\surd 2}$

by rationalising the denominator, we get x = $6-4\surd 2$

On going through the solution, you can see that the key concept is Pythagoras theorem and it involves the construction of joining the centres of the circles and their point of contact.

Now, the major takeaways from this problem should be:

1. Joining the centres of the circles and their point of contact
2. Locating the right angle triangles where we can apply Pythagoras theorem to get to the answer.

Assume that you have gone through the solution with the above takeaway, then you can apply similar approach to solve all of the following problems.

Question 2: Two semicircles are inscribed in the square as shown. If the side length of the square is 2 cm, find the radius of the smaller semicircle.

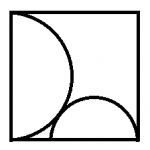
Approach:

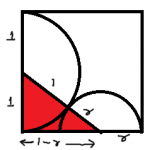
Observe that the two semicircles are tangent to each other, hence we can join their centres and point of tangent to get a right triangle as shown below. Now, we can apply Pythagoras theorem to get to the solution.

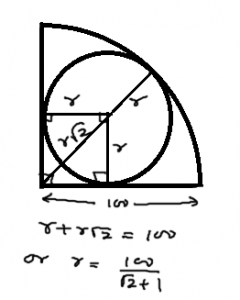
Question 3: If the radius of the quarter of the circle is 100 cm, find the radius of the circle inscribed in it.

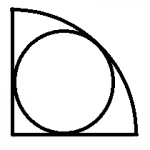
Approach:

Here are some other problems I am leaving them for you to solve. You can post the solution in the comment box below.

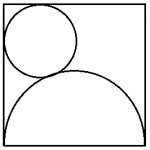
Question 4: If the side of the square is 10 cm, find the radius of the smaller circle.

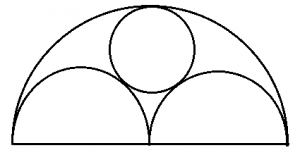
Question 5:  In the Figure given below, If the radius of the larger semicircle is R and the radius is smaller circle is r, find the ratio of r/R

Question 6: In the figure below, the rectangle at the corner measures 10 cm × 20 cm. The corner A of the rectangle is also a point on the circumference of the circle. What is the radius of the circle in cm?