Mensuration formulas based questions regularly feature in CAT, SSC CGL and other exams. Being a part of geometry, this topic demands that the aspirant be familiar not only with the different formulas of mensuration but also with the other theorems and concepts of geometry. However, the questions from mensuration are less difficult that other types of geometry questions.
An aspirant must be familiar with different mensuration concepts and geometrical concepts such as triangle, circle, rectangle, square, cone , cuboid, cube, cylinder, sphere. In addition to this, he must correctly remember the area, perimeter and volume formulae of different geometrical shapes. This article contains advance mensuration formulae and geometry shortcut tricks.
All Mensuration Formulas for Triangles:
It is the sum of all three sides of a triangle. Let a, b, and c be the sides of a triangles then:
- Formula of Perimeter of triangle (P) = a + b + c
- Formula of Semi Perimeter of triangle (s) =(frac{a+b+c}{2})
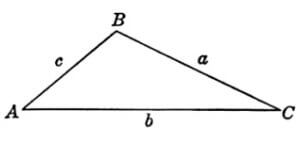
The two mostly used mensuration formulas for area of triangle are:
- Area of triangle =\(\frac{1}{2} \times b \times h\)
- Area of triangle =\(\sqrt {s\left( {s – a} \right)\left( {s – b} \right)\left( {s – c} \right)} \)
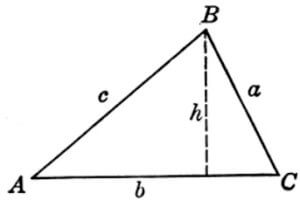
Some advance mensuration formulas for area of triangle are:
- Area of triangle =\(r \times s\), where \(r\) is in-radius of the triangle.
- Area of triangle = \(\frac{abc}{4R}\), where \(R\) is circum-radius of the triangle.
- Area of triangle=\(\frac{4}{3}\sqrt {u\left( {u – d} \right)\left( {u – e} \right)\left( {u – f} \right)} \)
,where d, e and f are medians and \(u = \frac{{d + e + f}}{2}\) - Area of triangle=\(\frac{1}{2} \times ab\sin \theta \), where a and b are the two known sides and is the included angle.
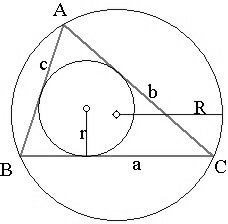
Some mensuration formulas for area of special triangle:
- Area of equilateral triangle =\(\frac{{\sqrt 3 }}{4}{a^2}\), where a is the side of the equilateral triangle
- Area of isosceles triangles =\(\sqrt {{a^2} – \frac{{{b^2}}}{4}} \), where a be the measure of the equal sides of an isosceles triangle and b be the base of the isosceles triangle.

Mensuration Formulas for Circles
Circumference of circle=\(2\pi r\)
Area of circle=\(\pi {r^2}\)
Length of arc=\(\frac{\theta }{{360}} \times 2\pi r\)
Area of Sector=\(\frac{\theta }{{360}} \times \pi {r^2}\)
Area of Segment=\(\frac{\theta }{{360}} \times \pi {r^2} – \frac{1}{2} \times {r^2} \times \sin \theta \)

Mensuration Formulas for Quadrilaterals
- Area of any Quadrilateral =\(\frac{1}{2} \times one\;diagonal \times \left( {h1 + h2} \right)\)
- Area of any Quadrilateral = \(\frac{1}{2}\)×d1d2×sinθ, where d1 and d2 are the diagonals of the quadrilaterals and ‘θ’ is the angle between them
- Area of any Quadrilateral = \(\sqrt {(s – a)(s – b)(s – c)(s – d) – abcd \times {{\cos }^2}\alpha } \), where \(\alpha \)= Average of any pair of opposite angles of the quadrilateral and \(s = \frac{{a + b + c + d}}{2}\)
- Perimeter of Rectangle = 2(length+breadth)
- Area of Rectangle=length x breadth
- Perimeter of Square=4a
- Area of Square = \(a^2\), where \(a\) is the side of the square.
- Perimeter of Parallelogram =2(a+b), where a and b are two adjacent sides of the parallelogram.
- Area of Parallelogram=base x height
- Perimeter of Rhombus = 4a
- Area of Rhombus = \(\frac{1}{2}\times {{d}_{1}}\times {{d}_{2}}\), where d1 and d2 are the two diagonals of the Rhombus.
- Area of Trapezium=\(\frac{1}{2}\times \left( a+b \right)\times h\), where \(a\) and \(b\) are the parallel sides of the trapezium and \(h\) is the perpendicular distance between \(a\) and \(b\).
Important Trick:
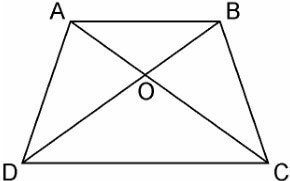
In any trapezium ABCD, with AC and BD as diagonals intersecting at O, then
Let Area of ∆ AOD = ∆ BOC
Also, we have the following relations:
Area of ∆ AOB x Area of ∆ COD = Area of ∆ BOC x Area of ∆ AOD
A quadrilateral is said to be a cyclic quadrilateral if there is a circle passing through all its four vertices.
- Area = \(\sqrt{(s-a)(s-b)(s-c)(s-d)}\)
- Sum of the opposite angles of a cyclic quadrilateral is 180°
- If a pair of opposite angles of a quadrilateral is supplementary, then the quadrilateral is cyclic.
- Ptolemy’s Theorem: A a cyclic quadrilateral with consecutive sides a, b, c, d and diagonals p, q is cyclic if and only if ac + bd = pq.


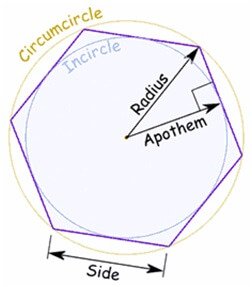
Mensuration Formulas for Polygons
The area of a regular polygon is given by the formula below.
Area =\(\frac{1}{2}\) (apothem)(perimeter)
Regular Polygon Formulas
n = number of sides
s = length of a side
r = apothem (radius of inscribed circle)
R = radius of circumcircle
Several other area formulas:
Sum of interior angles = (n – 2)·180°
Interior angle =\(\frac{\left( n-2 \right)}{n}\times {{180}^{0}}\) for regular polygons
Exterior angle =\(\frac{{{360}^{0}}}{n}\) for regular polygons
Mensuration Formulas for Solid (3D) Geometry
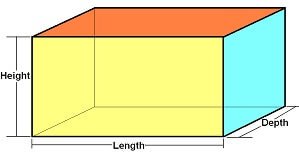
Mensuration Formulas for Cuboid
Total Surface Area of Cuboid =2(lw + lh + wh), where l = length, w = width, h = height
Volume of Cuboid=lwh, where l = length, w = width, h = height
Mensuration Formulas for Cube
Total Surface Area of Cube=\(6a^2\)
Volume of Cube=\(a^3\)
here \(a\) is edge length of the cube.

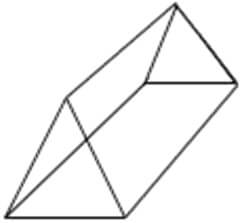
Mensuration Formulas for Prism
Lateral Surface Area of Prism=perimeter of base × heightTotal Surface Area of Prism = 2 × area of base + perimeter of base × height
Volume of Prism = area of base x height
See Also: Solid Geometry – Prism and Pyramid
Mensuration Formulas for Pyramid
Lateral Surface Area of Pyramid=\(\frac{1}{2}\times\) perimeter of base × slant height
Total Surface Area of Pyramid= area of base + area of base + \(\frac{1}{2}\times\) perimeter of base × slant height
Volume of Pyramid= \(\frac{1}{3}\times\)area of base x height

Mensuration Formulas for Cylinder
Curved Surface Area of Cylinder=\(\2 \times\ pi rh\)
Surface Area of Cylinder=\(2\pi r\left( {r + h} \right)\)
Volume of Cylinder=\( \pi {{r}^{2}}h\)

Mensuration Formulas of Cone
Curved Surface Area of Cone=\(\pi rl\) , whe l = slant height
Total Surface Area of Cone=\(\pi r\left( {r + l} \right)\)
Volume of Cone=\(\frac{1}{3}\pi {r^2}h\)

Mensuration Formulas of Sphere
Total Surface Area of Sphere =\(4\pi {r^2}\)
Volume of Sphere=\(\frac{4}{3} \times \pi {r^3}\)

Mensuration Formulas of Hemisphere
Curved Surface Area of Hemisphere=\(2\pi {r^2}\)
Total Surface Area of Hemisphere =\(3\pi {r^2}\)
Volume of Hemisphere=\(\frac{2}{3} \times \pi {r^3}\)









3 Responses
i love the the way its explaining
Volume of pyramid is 1/3 bh
It is well explanatory and educative